För omkring tre hundra år sedan, då man övergick till att tillverka besman av järn, förbjöd myndigheterna användning av den äldre typen av trä eftersom de var alltför opålitliga. Det besman jag nu ska berätta om är mycket speciellt. Det är av trä, det är tillverkat 1801 och det är krönt och kontrollerat av viktinspektören P Wikström. Konstruktionen påminner om de besman av järn som man ännu så sent som på 1970-talet kunde se i torghandeln - men som sagt, här är det frågan om ett besman av trä.

På besmanets vågbalk löper ett metallbeslag och på det beslaget sitter ett rejält handtag. På vågbalkens ovansida finns en skala utförd i färgtryck och den är graderad i lod (och fjärdedels lod, dvs kvintin). Efter 32 lod är graderingen i skålpund (32 lod = 1 skålpund). Vidare har besmanet både vågskål och krok. På så vis kan man väga både småsaker, t ex kryddor och tyngre saker. Att besmanet är tillverkat av trä har nog sin förklaring. Det verkar ju vara ett kryddbesman, dvs ett specialbesman för låga vikter. Kryddbesman av trä var ganska vanliga under första halvan av 1800-talet. Det exemplar som här beskrivs är ändå lite speciellt eftersom det klarar av att väga med en upplösning av halva kvintin (c:a 1,5 gram) i början på vågbalken.

Ett förnämligt besman. Lämpligt för kryddor och medicin. Det är ett ganska litet besman. Dess längd är bara 345 mm.

Det som ger vågen precision är skalan på vågbalkens översida och metallbeslaget som löper utmed vågbalken. Metallbeslaget lägger grunden för att finna en exakt jämviktspunkt samt möjlighet att läsa av skalan på vågbalkens översida med tämligen god exakthet.

Beslaget som löper utmed vågbalken och den lättavläsliga skalan lägger grunden för precisionen.

Skalan som är tryckt på vågbalkens översida är i början på vågbalken graderad i lod och den första markeringen är indelad i åttondels lod, dvs halva kvintin (~1,5 gram). Efter 32 lod är skalan graderad i skålpund upp till 4 skålpund.

Skiss av vågbalkens översida i skala 1:1.

Skalan närmast "klunsen" i närbild.

Skalan i närbild några centimeter ut på vågbalken.

Matematiken bakom besmanets funktion

Besmanets funktion kan beskrivas med följande figur:

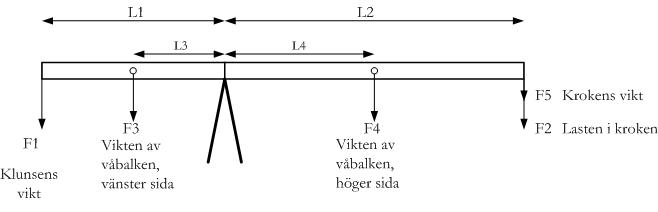
Den generella formeln för jämvikt ser ut så här:

L1 * F1 + F3 * L3   =   L2 * F2 + F4 * l4 + F5 * L2

L2 = Ltot - L1

En konstant k sätts in som ett mått på vågbalkens vikt per längdenhet.

F3 = k * L1        F4 = k * L2

L3 = ½ * L1       L4 = ½ * L2

Den generella formeln kan skrivas på följande sätt:
 

   
 

Formeln beskriver hur L1 beror av F2, dvs var på vågbalken jämvikt uppnås vid olika laster i kroken.

Om du vill se hur jag kommit fram till formeln     << klicka här >>

Genom att sätta in lämpliga värden på Ltot, F1, F5 och K samt presentera resultatet grafiskt, ser vi att det råder ett olinjärt samband mellan L1 och F2. Kurvorna närmar sig vågbalkens längd asymptotiskt.

Klunsens vikt (F1) har satts till 1000 gram.

Vågbalkens längd (Ltot) har satts till 1000 mm.

Krokens vikt (F5) har satts till 30 gram.

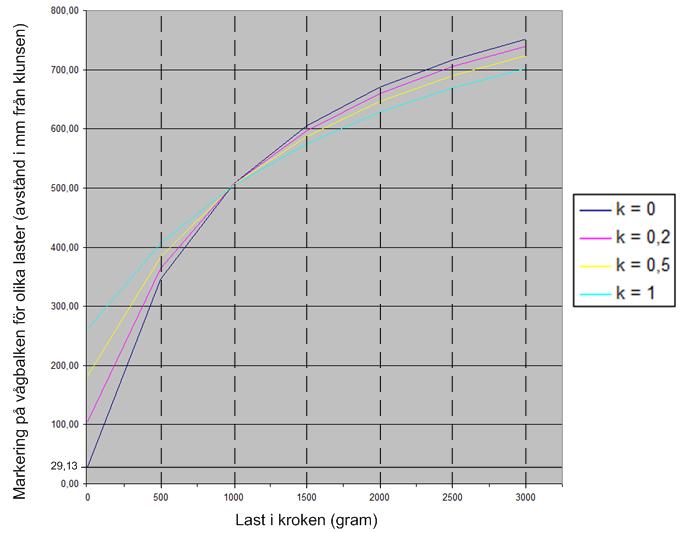
Den mörkblå kurvan har k=0, dvs vågbalken har ingen massa. Kurvan startar 29,13 mm från klunsen beroende på den tomma krokens vikt.

Den röda kurvan har k=0,2. Vågbalken väger då 200 gram, dvs en femtedel av klunsen. Jämvikt vid tom krok råder på avståndet 105,69 mm från klunsen.

Den gula kurvan har k=0,5. Vågbalken väger då 500 gram, dvs hälften av klunsen. Jämvikt vid tom krok råder på avstånedet 183,01 mm från klunsen.

Den ljusblå kurvan har k=1. Vågbalken väger därmed lika mycket som klunsen. Jämvikt vid tom krok råder på avståndet 261,08 mm från klunsen.

Några kommentarer till ovanstående

Eftersom lutningen på kurvorna är störst närmast klunsen blir också avståndet mellan skalans markeringar större där, dvs besmanet har högst upplösning närmast klunsen.

Det som inverkar på upplösningen är både klunsens vikt och vågbalkens vikt, hela besmanets vikt påverkar således upplösningen. Vågbalkens längd påverkar upplösningen i viss mån. Detta utvecklas ytterligare nedan under rubriken "Ett fjäderlätt besman".

Att använda trä för tillverkning av besman verkar vara en god ide om man vill uppnå hög precision eftersom besmanets totala vikt på så vis kan hållas låg. Detta är orsaken till att kryddbesmanen gjordes av trä i början av 1800-talet.

Foto: Gunnar von Köhler, Los Angeles, Kalifornien.

Text: Lennart Castenhag

Ett fjäderlätt besman

Ett bevis för att ett lätt besman har hög upplösning

Antag att vi lyckas konstruera ett besman som väger mindre än 10 gram, med följande data:

  -   Klunsens vikt 7,80 gram
  -   Vågbalkens längd 245 mm
  -   Vågbalkens vikt 1,70 gram

Ett sådant besman skulle bli en perfekt brevvåg. Se följande figur:

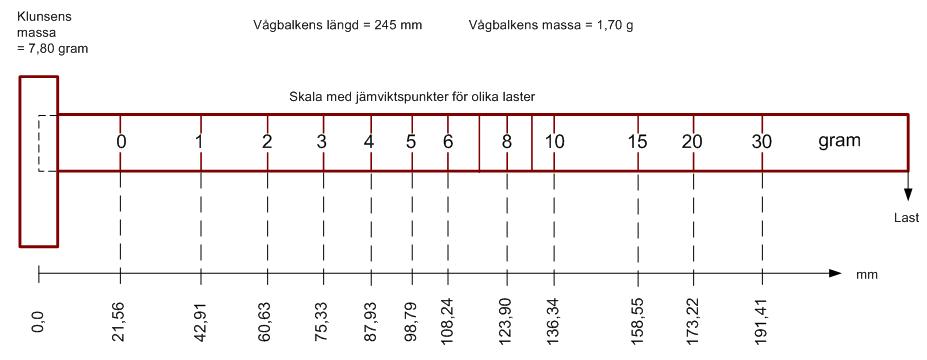
En skiss på ett besman för att väga laster på upp till 30 gram. Skiss i naturlig skala.

Avståndet mellan skalstrecken i ovanstående skiss är över 1 cm i början på vågbalken -
och varje skalstreck motsvarar 1 gram.

Med hjälp av en grillpinne och ett suddigummi lyckades jag tillverka ett sådant besman.

Ett fjäderlätt besman. Total vikt 9,5 gram.

Tester med labuppkopplingen enligt bilden visar att teorin stämmer. Vid olika laster blir jämviktspunkten precis enligt vad som beräknats i den teoretiska skissen.

Det är bara en nackdel med detta besman. Den är lite "fnulig" att hantera. En modern digital brevvåg har absolut sina fördelar.

Text och foto: Lennart Castenhag

Dokumenthistorik

2011-07-10   Kompletterat med teoretiskt fjäderlätt besman

2011-07-09   Besmanets matematik vidareutvecklat

2011-06-30   Kompletterat med besmanets längd samt besmanets matematik

2011-06-29   En första utgåva